[图论]匹配

匹配通俗的说就是配对，抽象讲就是图边集的一个子集。

相关概念

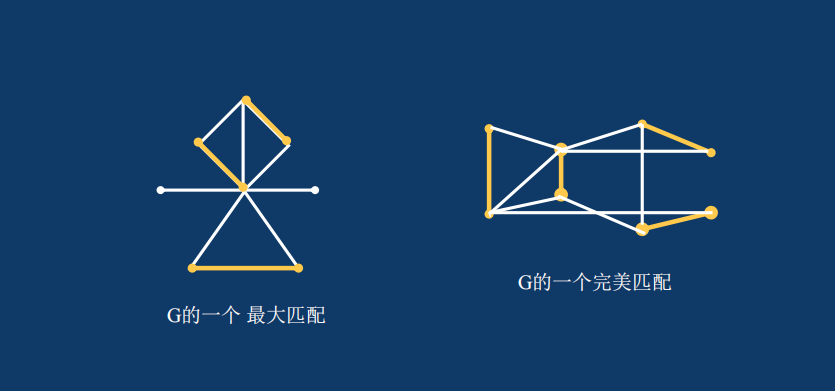
• 匹配：图$G$的边子集$M$（不含环）是$G$的一个匹配，如果$M$中的边两两不邻接。
• M饱和点：如果一个顶点在匹配$M$中有边与之关联，那么称这个顶点是$M$饱和的。非饱和点反之。 $M$饱和点是相对的，可能在另一个匹配中是非饱和点。
• 最大匹配：图$G$中边数最多的匹配。

• 完美匹配：如果一个最大匹配$M$饱和了$G$中的所有顶点，那么称$M$是$G$的一个完美匹配。

  一个图中不一定有完美匹配。

  

• M交错路：设$M$是图$G$的一个匹配，如果$P$是一条$M$中边和不在$M$中的边交替出现的路，那么称$P$是$M$交错路。
• M可增广路（M可扩路）：设$p$是一个$M$交错路，$P$的起点和终点都不在$M$中，那么称$P$是$M$可增广路。

相关性质与定理

• 匹配定理：设$M$是图$G$的一个匹配，$P$是$M$可增广路，那么$M_1 = M\oplus P$是$G$的一个更大的匹配。这体现了可增广路的增广性质。 $M\oplus P = (M-P)\cup(P-M)$

  

  以下是对图片的详细说明，看不懂的可以参考一下（前两种情况好懂，第三种情况对照着下面图解释来看）： 要证M1 是 G的匹配， 需证三个方面：

  1. M-E（P）中的任意两边不相邻：显然，M本身任意两边不相邻，除去一个集合后仍然满足；

  2. E（P）-M中的任意两边不相邻：显然，M是不相邻的边，P是完整通路，完整通路除去不相邻的边，剩下的也不相邻；

  3. M-E（P）中的任意一边和E（P）-M中的任意一边不相邻：

  （1） 对于E(P)-M中的含有P首尾两端点的边： 由于P是可扩路，首尾两端点是非饱和的，因此M-E(P)不包含首尾两端点，且由于P是首尾两端点之间的通路，M-E(P)一定把与首尾两个边相邻的可能给减掉了，因此E(P)-M中的含有P首尾两端点的边不可能在M-E(P)有相邻的边；

  （2）对于E(P)-M中的不含有P首尾两端点的边： 除去含有首尾端点的边，E(P)-M中的所有顶点都是M饱和点，形成的边是与原来$M$完全不同的“交错的边”，而如果有与这样交错边相邻的边，一定是原来M中的边，但是M-E(P)中不含有这些可能与“交错的边”相邻的M中原来的边（因为P一定有M中原来的边，M-P的时候减掉了）。

  综上所述，M1是G的匹配。

  

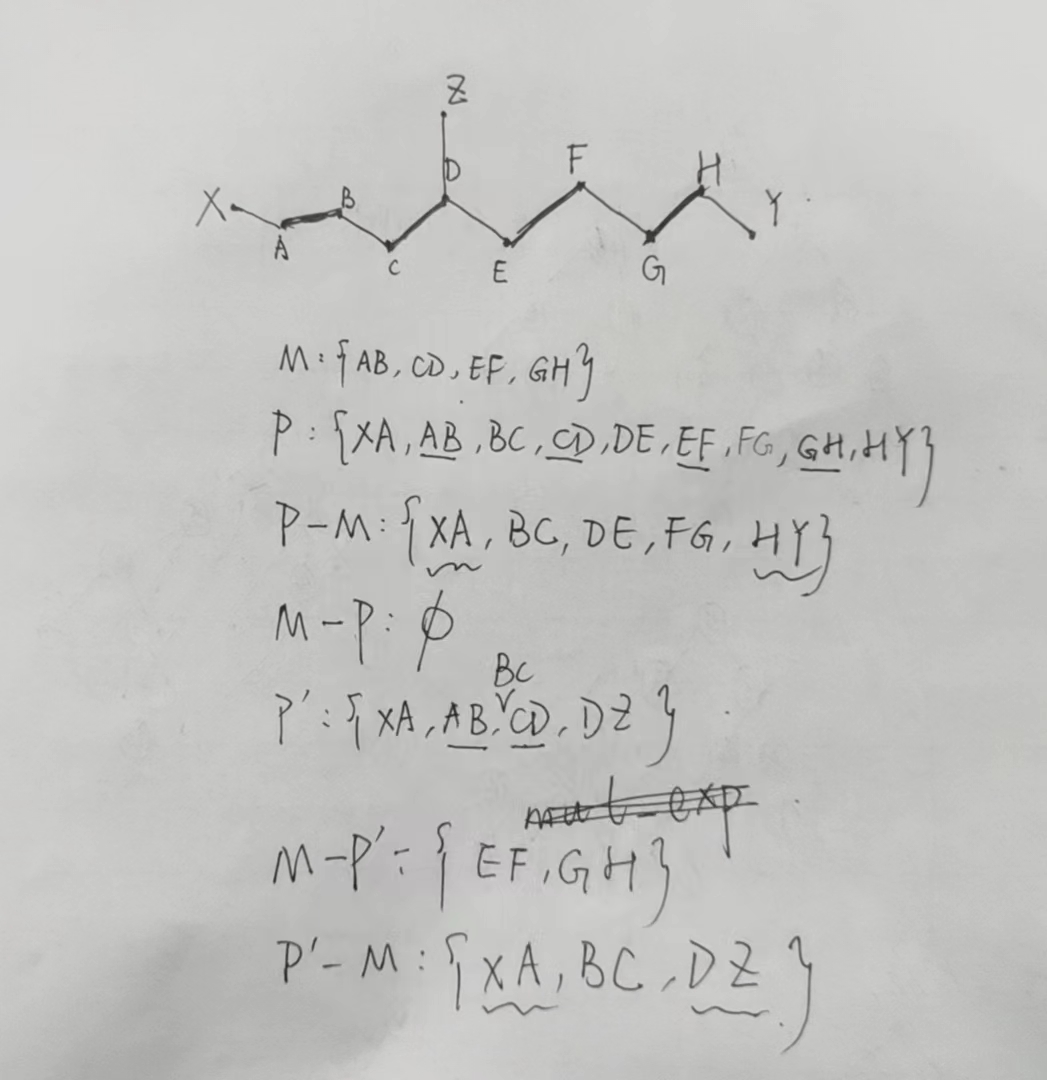
  最初写的P包括了M的全部，是对M交错路理解不深导致的，其实可以只取M的子集，形成交错路，以下是对图片的详细解释

  注意看P’，是X到Z的一条通路。

  对于讨论（1），其中$XA$和$DZ$在$M-P’$中是一定没有相邻的边的，因为如果有，那只能是$AB$或者$DC$，但是$AB$和$DC$一定属于$P’$（你要从$X$走到$Z$），所以$M-E(P’)$就减掉了，因此$XA$和$DZ$不可能在$E(P’)-M$中有相邻的边；

  对于讨论（2），因为$E(P’)-M$除了首尾边之外，一定是$M$的“交错的边”如$BC$（就是虽然每个边的两个端点是$M$饱和点，但并不是$M$匹配），因此如果有与这些“交错的边”相邻的，一定只能是$M$中的边，然而在$M-E(P’)$中，$M$中相对应的边已经被减去了（$E(P’)$中含有$AB$与$CD$。$P’$是$X$到$Z$的通路，由于$BC$存在于$E(P’)$，因此$AB$和$CD$必然存在于$E(P’)$），因此$E(P’)-M$中的边不可能与$M-E(P’)$中的边相邻。

• 贝尔热定理 : $G$的匹配$M$是最大匹配，当且仅当$G$不存在$M$可扩路

  证明：

  1.必要性：$M$ 是最大匹配，不存在 $M$ 可扩充路。逆否命题:存在可扩充路，就不是最大匹配 ： 假设存在有$M$可扩路$P$，那么$M\oplus P$是一个更大的匹配，所以$M$不是最大匹配，得证。

  2. 充分性：不存在 $M$ 可扩充路，$M$ 是最大匹配。反证法：假设$M$ 不存在可扩充路，但是$M$ 不是最大匹配 ： 设一个最大匹配为$M’$,$ \vert M’ \vert >\vert M \vert $ ，那么$M’\oplus M$ 中一定存在$M$可扩路$P$，与假设矛盾，得证。

  详细解释：首先要明确的是，$M’$与$M$是否可能存在重合的边？不可能，如果有，那么$M’$不可能是最大匹配。

  第一种情况：它可以把$M$中与它自己不重合的边取出，构成一个更大的匹配。

  第二种情况： 产生不了更大的匹配了，但是我们可以发现矛盾，存在$M$的可扩路，不满足条件；

  以下的分析建立在$M’$与$M$没有重合的边的基础上：

  情况1： 如果两个匹配完全不相邻, 那么并起来是个更大的匹配，不符合$M’$是最大匹配的条件；

  情况2：如果两个匹配相邻，直接并起来不能形成匹配 ，那么我们做并集后，其中一定含有$M$的可扩路，与假设矛盾。得证。

  详细解释配图:

  

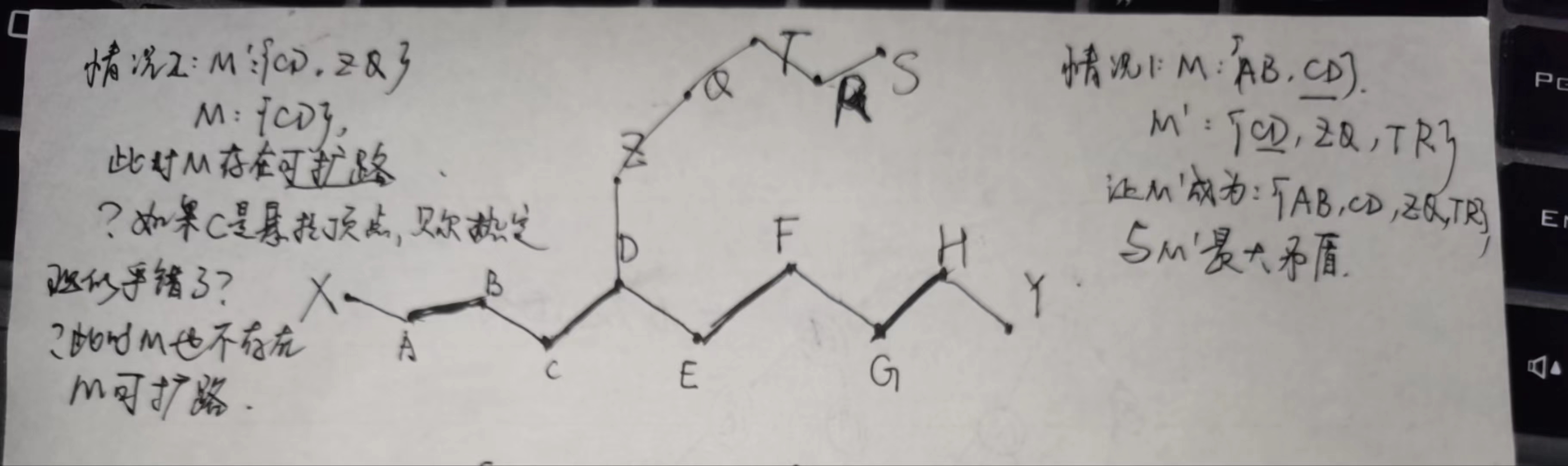
  其中存在一个关于贝尔热定理的问题，准备请教老师

  后面两种情况1，2好理解，就不配图了。

感谢阅读，祝你拥有愉快的一天！
爱来自：SakuraMarble
转载或引用请标注来源，欢迎评论！