[图论]托特定理与彼得森定理

托特定理是用来证明一般图的完美匹配的存在性的，而彼得森定理是托特定理的推论，用来证明没有割边的3正则图的完美匹配，彼得森定理也有推论，可以用来证明顶点数为偶数的k正则k-1边连通图有完美匹配

托特定理

• 托特定理：图$G$有完美匹配，当且仅当对$V$的任意真子集$S$，有：

  \[o(G-S) \leq |S|\]

  其中$o(G-S)$是$G-S$的奇分支数。

• 奇分支：奇分支是指顶点数目为奇数的连通分支。

彼得森定理

• 彼得森定理：没有割边的3正则图有完美匹配。
• 割边：如果去掉一条边后，图不再连通，那么这条边就是割边。
• k正则图：每个顶点的度数都是k的图。

• 证明：还是利用托特定理来证明。

  3正则图的顶点数为什么是偶数？设边的数目为$m$，顶点数目为$n$，根据握手定理$2m = 3n$，$m = \frac{3n}{2}$，由于$m$是整数，所以$n$一定是偶数。

  1. $S$为空集时，由于$G$是3正则图，所以$\vert V \vert $为偶数（如遗忘如何证明可参考上方卡片）。那么$o(G-S) = o(G) = 0 \leq \vert S \vert = 0$，满足托特定理（第一个等号根据S是空集，第二个等号根据顶点数目是偶数）。
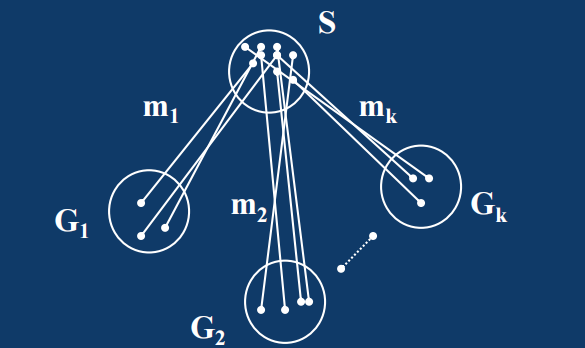
  2. $S$不为空集时。
     1. 设$G_1,G_2,…,G_k$是$G-S$的所有奇分支。$m_i$表示端点分别属于$S$和$G_i$的边数。
     2. 下面分析$m_i$，此处统一使用了一个思想，把一个图中的度数视作图内部贡献的与图外部贡献的两个部分。
     3. 在$G_i$中，内部贡献的度数为$2\vert E(G_i) \vert $（根据握手定理）；把视野放大，看$G_i$在整个$G$中的总度数为$3\vert V(G_i) \vert $（3正则图）。所以有$m_i = 3\vert V(G_i)\vert - 2\vert E (G_i) \vert$，根据$\vert V(G_i) \vert$ 是奇数（因为是奇分支），而$2 \vert E(G_i) \vert $一定是偶数，所以可以得到$m_i$是奇数。又因为$G$没有割边，因此作为沟通不同分支的$m_i$不可能为1，所以$m_i \geq 3$，这样就有
  \[o(G-S) = k \leq \frac{1}{3} \sum_{i=1}^{k}m_i \leq \frac{1}{3} \sum_{v \in S}d(v) = \frac{1}{3} \cdot 3\vert S\vert = \vert S \vert\]

  第二个不等号是因为$S$的度数是由$S$内部度数和$m_i$提供的度数，以及偶分支提供的度数构成的，因此肯定大于只有$m_i$提供的度数，第三个不等号是因为$G$是3正则图。

  这里本来是寻找奇分支数和顶点数目之间的一个不等关系，首先将奇分支数通过与$S$之间的连边数与奇分支数之间的倍数关系建立联系，转化为求边数目与顶点数目之间的联系，然后又对$S$度数贡献来源的分析，把边数目与S的度数建立联系，这下问题转化为求S的度数与S的顶点数目之间的联系，根据正则图的定义，发现其中的倍数关系，成功建立联系。

  1. 综上，$o(G-S) \leq \vert S \vert$，满足托特定理，因此没有割边的3正则图有完美匹配。

彼得森定理推论

• 彼得森定理推论：设$G$是顶点数为偶数的k正则k-1边连通图，那么$G$有完美匹配。

  注意只是一个充分条件

• k-1边连通图：去掉k-1条边后，图才不再连通。

• 证明： 类似于彼得森定理本身，只需要证明$m_i \geq k$就行。

  对于S是空集的情况我们略去了，和之前类似。

  1. 因为是k-1连通图，所以$m_i \geq k-1$，如何提升$k-1$ 至$k$呢？根据之前类似的方式 $ m_i = k \cdot \vert V(G_i)\vert - 2\vert E(G_i)\vert $，$m_i$的奇偶性完全由$k$来决定，$k$是奇数，$m_i$就是奇数，否则是偶数。
     1. 假设$k$为奇数，那么$m_i$就为奇数，而$k-1$是偶数，所以根据之前说的$m_i \geq k-1$，$m_i$的最小值是$k$
     2. 假设$k$为偶数那么$m_i$就是偶数，而$k-1$是奇数，所以根据之前的$m_i \geq k-1$，$m_i$最小值不可能取$k-1$，只能是$k$
     3. 综上所述，得证$m_i \geq k$
  2. 根据之前得到$m_i \geq 3$的类似套路，接下来使用托特定理:
  \[o(G-S) = t \leq \frac{1}{k} \sum_{i=1}^{t}m_i \leq \frac{1}{k} \sum_{v \in S}d(v) = \frac{1}{k} \cdot k\vert S\vert = \vert S \vert\]

  由托特定理，得证$G$存在完美匹配

树上完美匹配存在性定理

• 内容： 一棵树$G$有完美匹配，当且仅当对所有的顶点$v$，有：$o(G-v) = 1$

  这与托特定理不同之处在于：托特定理要求图中任意一个真子集都满足一个不等关系，而这里是任意一个点满足一个等量关系。

• 证明：

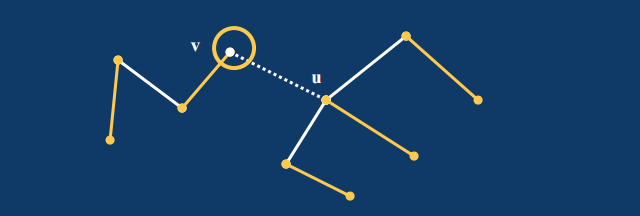
  必要性：

  1. 因为有完美匹配，由托特定理，$o(G-S) \leq \vert S \vert $ 对任意$S$ 都成立，那么我们取$S$ 为单个的点，因此有$o(G-v) \leq 1$；

  2. 因为有完美匹配，所以树的顶点数目必须为偶数，假设$o(G-v)$为0，那么，与$v$相邻的是两个偶分支，总共树的顶点数为奇，与条件矛盾。因此$o(G-v) \geq 1$

  3. 得证$o(G-v) = 1$

  充分性：

  1. 条件：对任意顶点$v \in V(G)$,有$o(G-v) = 1$。

  2. 设$G_v$为$G-v$唯一的奇分支，又设$G$中由$v$连到$G_v$的边为$vu$，由$u$连到$G-u$的奇分支$G_u$的边也是$uv$（整棵树就是两个奇分支拼起来的）。

  3. 令$M = {e(v):由v连到G_v的边，v \in V(G)}$，由每一个$v$都会存在这样的边将其饱和，因此$M$就是一个$G$的完美匹配

---

感谢阅读，祝你拥有愉快的一天！
爱来自：SakuraMarble
转载或引用请标注来源，欢迎评论！